Pattern recognition#
Learning Objectives#
Understand the concept of pattern recognition and its importance in problem-solving
Identify and utilize patterns to simplify complex problems
Recognize patterns in various contexts, including mathematical sequences and real-world applications
Use iteration to automate repetitive tasks based on identified patterns
Overview#
Pattern recognition involves finding the similarities or patterns among small, decomposed problems that can help us solve complex problems more efficiently. Once a problem has been broken down into simpler sub-problems, there may be similarities among these that mean we do not have to write a solution twice. These patterns may exist both between and within individual problems.
Sometimes the redundancy is really obvious to spot.
For example, let’s say we want to calculate the first 5 square numbers. This involves 5 sums:
1*1
2*2
3*3
4*4
5*5
For each number we are doing the same thing: multiplying it by itself. We can easily take advantage of that fact to write a function, or use a for loop or similar construct.
Sometimes it’s harder to define a pattern.
For example let’s say we want to calculate the first 5 triangular numbers. This involves 5 sums:
1
1+2
1+2+3
1+2+3+4
1+2+3+4+5
We can see a pattern here but it’s not as simple as the square number example. It is a pattern of two stages: first we need to create a list or sequence of the numbers, before we can sum them. Now that we have identified the pattern, we can try to construct some code to automate/simplify its implementation.
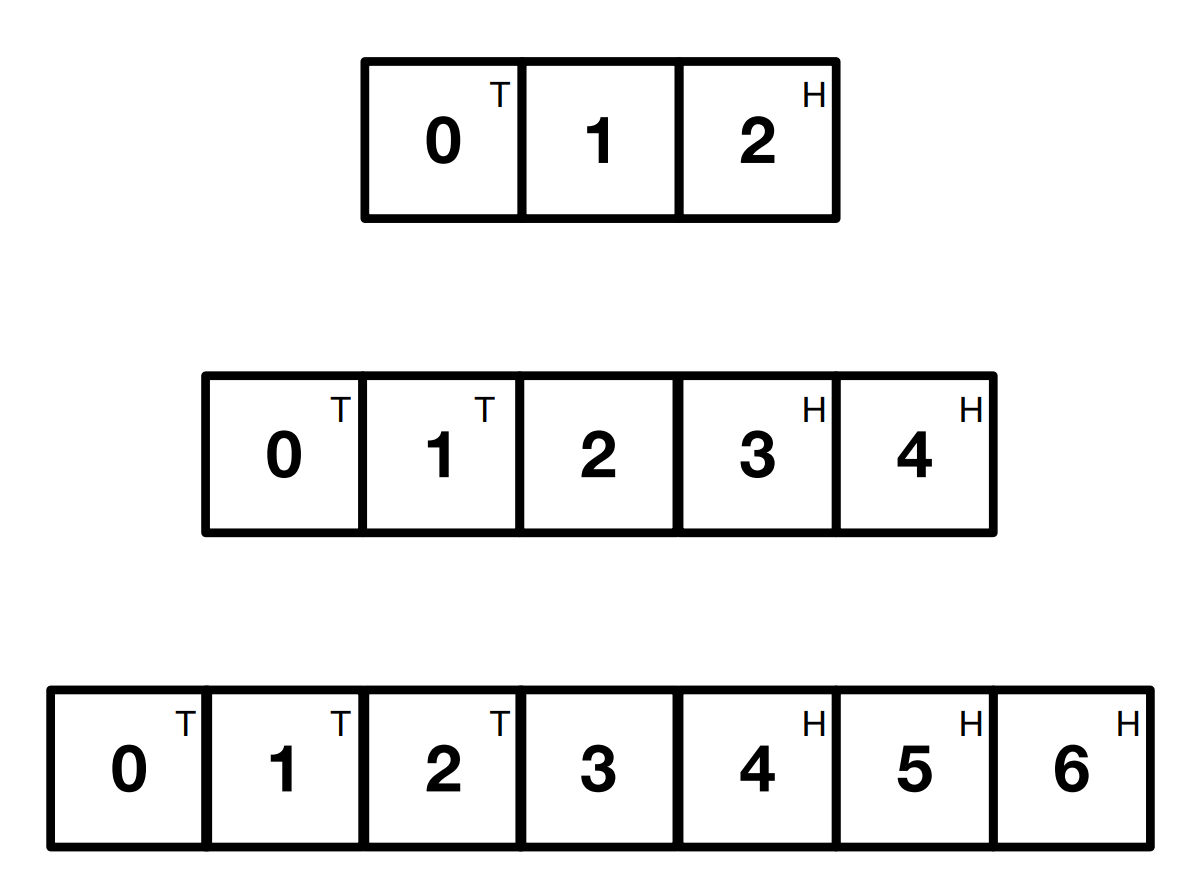
Activity: The swap puzzle#
Place small coins heads up on the squares marked H and tails up on the squares marked T. Swap the positions of the Heads for the Tails in as few moves as possible.
There are two ways to move a piece:
Move left or right to an adjacent empty square
Jump over a single adjacent piece into an empty space.
There are three increasingly larger boards that get harder. Complete the first in 3 moves, the second in 8 moves and the third in 15 moves.
Can you identify the pattern for a general solution for each board?
Activity: Lost in translation#
Here’s a simple real-world application from the field of bioinformatics. Genetic information is stored in DNA, which is a sequence of 4 bases (the nucleotides, conventionally indicated by the uppercase letters A, C, T, G). Thus a part of a gene might look like the string “GATTACA”. During translation, molecular machinery converts the genetic sequence to a string of amino acids constituting a protein. In particular, DNA is read as a sequence of three-letter long “words” (the codons), each of which identifies an amino acid. So a sequence like “ATACAACCTGGTTCA” would be segmented as “(ATA)(CAA)(CCT)(GGT)(TCA)” and translated to “IQPGS”, according to the standard genetic code (see also the dictionary below). In reality, these sequences are a few thousand characters long, hence the need for a computational solution. Happily, if we discard all the chemistry, this is just straightforward string processing.
Design a program that takes a sequence of nucleotides (of any length) and translates it into amino acids. Use the genetic code table given below as a dictionary to look up the codons and perform the translation. How can you use the ideas of decomposition and pattern recognition to help you to write this? Is this similar to anything you have written before?
# The standard genetic code
gencode = {
'ATA':'I', 'ATC':'I', 'ATT':'I', 'ATG':'M',
'ACA':'T', 'ACC':'T', 'ACG':'T', 'ACT':'T',
'AAC':'N', 'AAT':'N', 'AAA':'K', 'AAG':'K',
'AGC':'S', 'AGT':'S', 'AGA':'R', 'AGG':'R',
'CTA':'L', 'CTC':'L', 'CTG':'L', 'CTT':'L',
'CCA':'P', 'CCC':'P', 'CCG':'P', 'CCT':'P',
'CAC':'H', 'CAT':'H', 'CAA':'Q', 'CAG':'Q',
'CGA':'R', 'CGC':'R', 'CGG':'R', 'CGT':'R',
'GTA':'V', 'GTC':'V', 'GTG':'V', 'GTT':'V',
'GCA':'A', 'GCC':'A', 'GCG':'A', 'GCT':'A',
'GAC':'D', 'GAT':'D', 'GAA':'E', 'GAG':'E',
'GGA':'G', 'GGC':'G', 'GGG':'G', 'GGT':'G',
'TCA':'S', 'TCC':'S', 'TCG':'S', 'TCT':'S',
'TTC':'F', 'TTT':'F', 'TTA':'L', 'TTG':'L',
'TAC':'Y', 'TAT':'Y', 'TAA':'_', 'TAG':'_',
'TGC':'C', 'TGT':'C', 'TGA':'_', 'TGG':'W'}
Credits: Flow Control-Exercises
Iteration#
Once you have recognised a pattern, this means you only need to write the code for this action once. You may either be able to reuse a previously written function to help solve a different problem, or it may be that you can iterate the same solution….

