Unsupervised learning

Learning objectives

• Recap what unsupervised learning is

• Explain how this relates to supervised learning, especially the main differences

• Perform K-means clustering, a simple unsupervised learning algorithm, on sample data

Recap

• In unsupervised learning, models learn from unlabelled data (i.e. without explicit supervision).

• The goal is to learn (often hidden) patterns or structures in the data.

• We use unsupervised learning for clustering, dimensionality reduction, anomaly detection, and more.

K-means clustering

• This type of algorithm tries to assign class labels (i.e. generate clusters) from unlabelled data.

• While there are many types of algorithms that generate clusters, K-means is a great place to start due to its simplicity (much like how we defaulted to linear regressions in previous notebooks).

How does it work?

The algorithm is quite simple. To generate k clusters from a dataset, it minimises the variance within each cluster.

1. Create k cluster centroids randomly

2. Assign each data point to the nearest centroid

3. Compute new centroids as the mean of the assigned points

4. Repeat steps 2 and 3 until the centroids stabilise (i.e. they do not move significantly)

omput

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

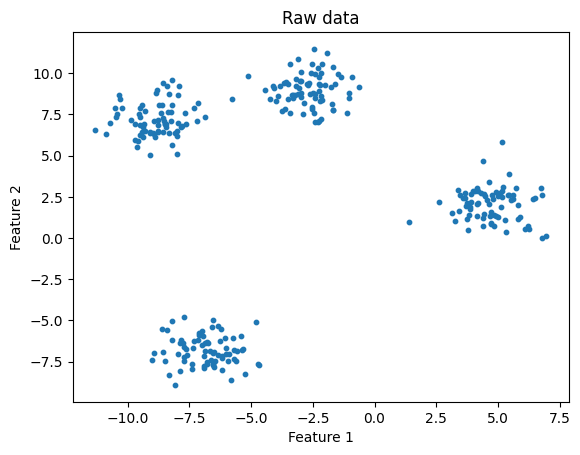
# Generate some data
X, y = make_blobs(n_samples=300, centers=4, cluster_std=1.0, random_state=42)

plt.scatter(X[:, 0], X[:, 1], s=10)
plt.title("Raw data")
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

def kmeans_and_plot(X, n_clusters, title):
    # Apply k-means
    kmeans = KMeans(n_clusters, random_state=42)
    kmeans.fit(X)
    y_kmeans = kmeans.predict(X)

    # Plot data coloured by k-means
    plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=10, cmap="viridis")
    plt.scatter(
        kmeans.cluster_centers_[:, 0],
        kmeans.cluster_centers_[:, 1],
        c="red",
        marker="X",
        s=100,
        label="Centroids",
    )
    plt.title(title)
    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    plt.legend()
    plt.show()

n_clusters = 4
title="K-means: Raw data coloured by predicted cluster"
kmeans_and_plot(X, n_clusters, title)

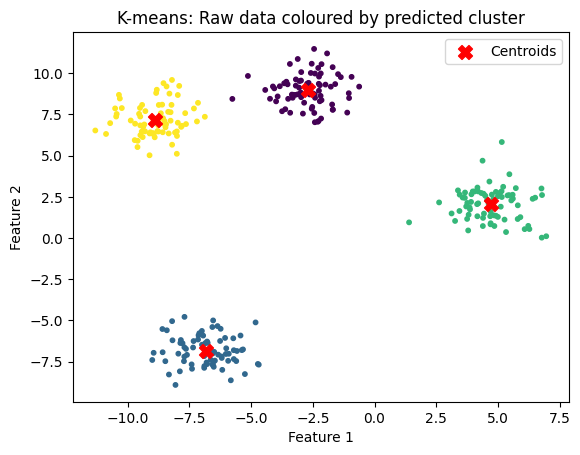
What happens if we have the wrong k?

• Here we could easily see 4 clusters, and specify k = 4.

• But what if we provide the wrong k?

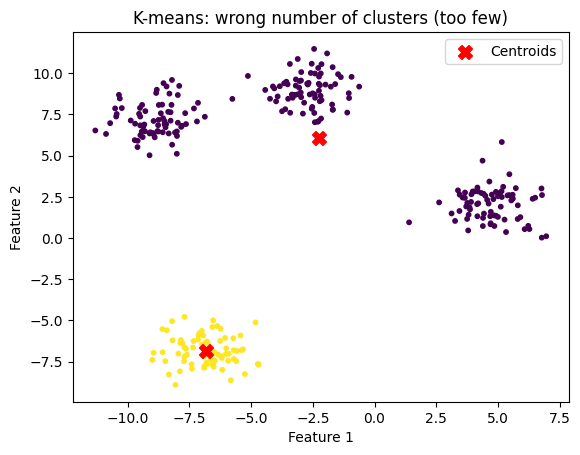
n_clusters = 2
title="K-means: wrong number of clusters (too few)"
kmeans_and_plot(X, n_clusters, title)

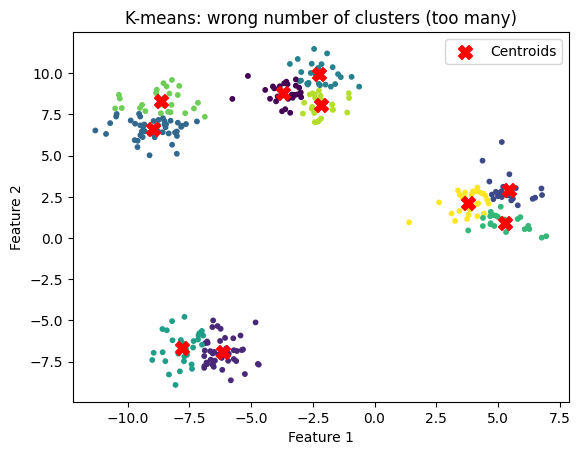
n_clusters = 10
title="K-means: wrong number of clusters (too many)"
kmeans_and_plot(X, n_clusters, title)

• Finally, what happens if we have a less distinct data set?

# Generate some data
X, y = make_blobs(n_samples=500, centers=10, cluster_std=2.0, random_state=42)

plt.scatter(X[:, 0], X[:, 1], s=10)
plt.title("Raw data")
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

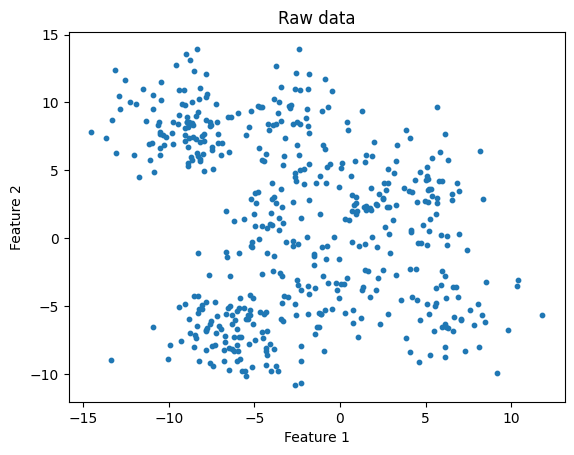
n_clusters = 10
title="K-means: correct number of clusters, less distinct clusters"
kmeans_and_plot(X, n_clusters, title)

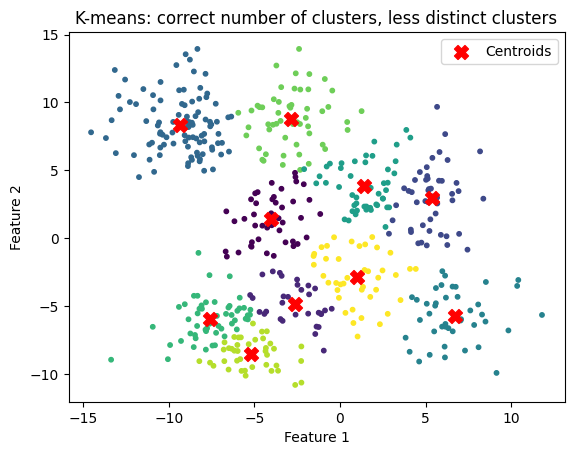
Determining the number of clusters

• We can attempt to calculate the number of clusters using the elbow method.

• This is not perfect, as shown below

# Generate some data
X, y = make_blobs(n_samples=500, centers=6, cluster_std=1., random_state=32)

plt.scatter(X[:, 0], X[:, 1], s=10)
plt.title("Raw data")
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

def elbow_method_and_plot(X, k_range, title, random_state=42):

    # Store within cluster sum of squares (inertia)
    wcss = []
    for k in k_range:
        kmeans = KMeans(n_clusters=k, random_state=random_state)
        kmeans.fit(X)

        # Store inertia
        wcss.append(kmeans.inertia_)

    # Plot the elbow curve
    plt.figure(figsize=(8, 5))
    plt.plot(k_range, wcss, marker='o', linestyle='-')
    plt.xlabel("Number of clusters k")
    plt.ylabel("Within cluster sum of squares (WCSS)")
    plt.title(title)
    plt.xticks(k_range)
    plt.show()

k_range = range(1, 11)
title = "Elbow method for finding k"
elbow_method_and_plot(X, k_range, title, random_state=42)

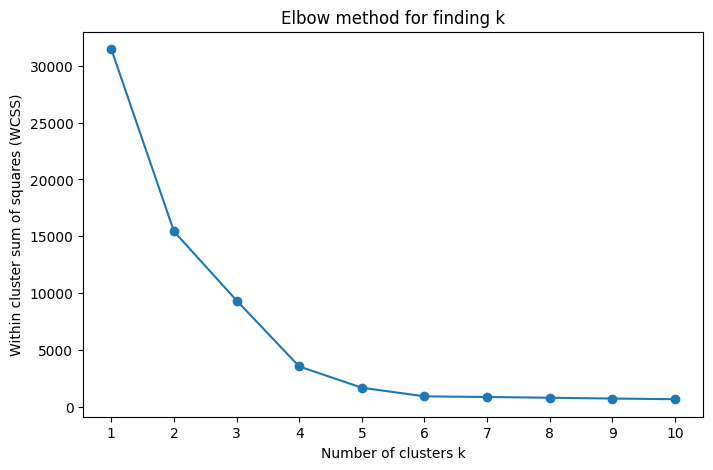
n_clusters = 5
title="K-means: data coloured by elbow method"
kmeans_and_plot(X, n_clusters, title)

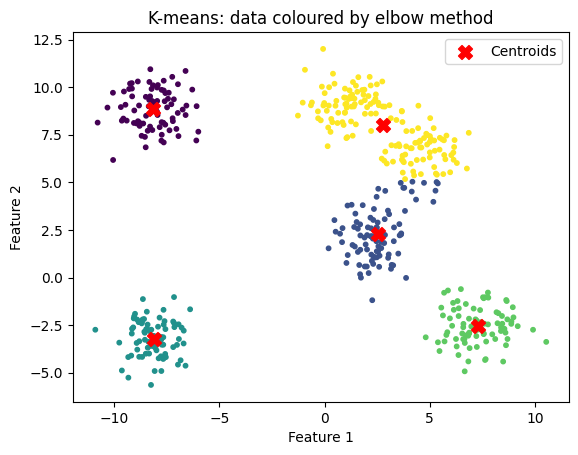
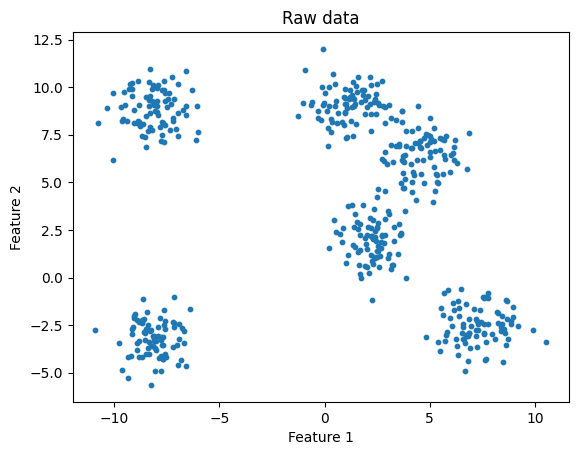
• When the clusters are less distinct, the elbow method might be less helpful:

# Generate some data
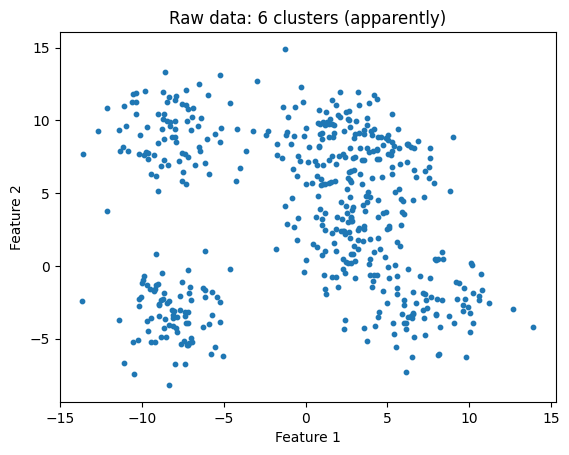
X, y = make_blobs(n_samples=500, centers=6, cluster_std=2, random_state=32)

plt.scatter(X[:, 0], X[:, 1], s=10)
plt.title("Raw data: 6 clusters (apparently)")
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

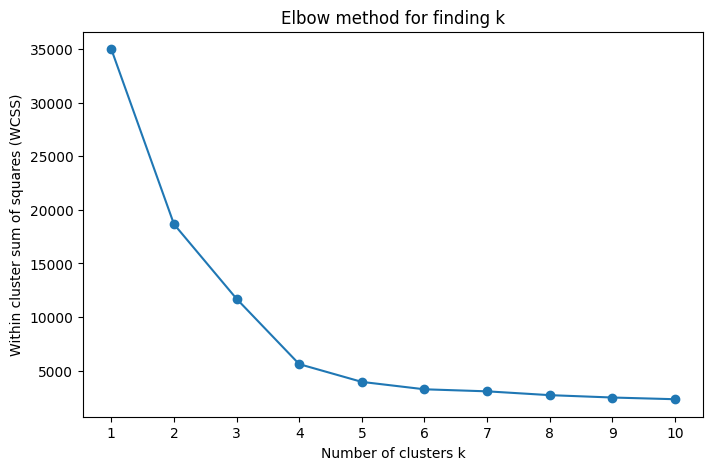
k_range = range(1, 11)
title = "Elbow method for finding k"
elbow_method_and_plot(X, k_range, title, random_state=42)

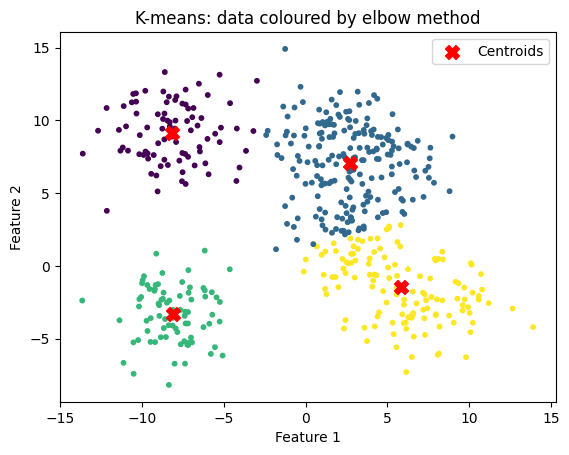
n_clusters = 4
title = "K-means: data coloured by elbow method"
kmeans_and_plot(X, n_clusters, title)

K-means Animation

Below is a animation of K-means, showing each iteration of the algorithm. Notice how the centroids get closer and closer to what a human might label as a ‘blob centre’ with each step. You should also notice how the centroids move in each iteration, they move to the centre of the points assigned to them.

The iframe contains an animated scatter illustrating K-Means over 10 iterations. Points update to their nearest centroid and centroids (red X) move each step.