Acceleration via Rcpp (advanced)

Acceleration via Rcpp (advanced)#

Overview#

C++ is a high-performance, general-purpose programming language that extends C with object-oriented, generic, and functional programming features. If you don’t know what those are, or have never used C++ before, do not worry. For us the most important point to note is that it can provide a fast alternative to R and can be integrated into our R code. In fact, under the hood, many of the base R functions are themselves written in C. In addition, many R packages on CRAN contain functions written in C++.

The easiest way to use C++ code in an R environment is through the Rcpp package. On MacOS and Linux systems, the Rcpp package is likely to be setup and loaded correctly after executing install.packages('Rcpp'), followed by library(Rcpp). On a windows OS, you may need to follow the instructions here to download Xtools.

You can check Rcpp is set up correctly by trying the following:

%%R
evalCpp("2+2")

[1] 4

Example: Estimating Pi#

Suppose we want to estimate the value of pi. One way of doing this is to use Monte Carlo sampling.

Consider a quarter-circle of radius 1 inside the unit square $ [0,1] \times [0,1].$ The equation for the quarter-circle is

$$x^2 + y^2 \leq 1.$$

Since the area of the full circle is $ \pi $, the quarter-circle has an area of $ \pi/4 $. By randomly sampling points inside the square and checking how many fall inside the quarter-circle, we can estimate $ \pi $ using:

$$ \pi \approx 4 \times \frac{M}{N} $$

where $ M $ is the number of points inside the quarter-circle, and $ N $ is the total number of points sampled.

We can plot this set-up:

%%R
# Define the quarter-circle function
theta <- seq(0, pi/2, length.out = 100)
x <- cos(theta)
y <- sin(theta)

samps <- runif(1000) |>
  matrix(ncol = 2)

inside <- samps[sqrt(rowSums(samps^2)) < 1,]
outside <- samps[sqrt(rowSums(samps^2)) >= 1,]

# Plot the quarter-circle
plot(x, y, type = "l", lwd = 2, col = 1, xlim = c(0,1), ylim = c(0,1),
     xlab = "x", ylab = "y", main = "Estimating Pi",
     xpd = FALSE, bty='l')
points(x = inside[,1], y = inside[,2], pch = 20, col = 1)
points(x = outside[,1], y = outside[,2], pch = 20, col = 2)
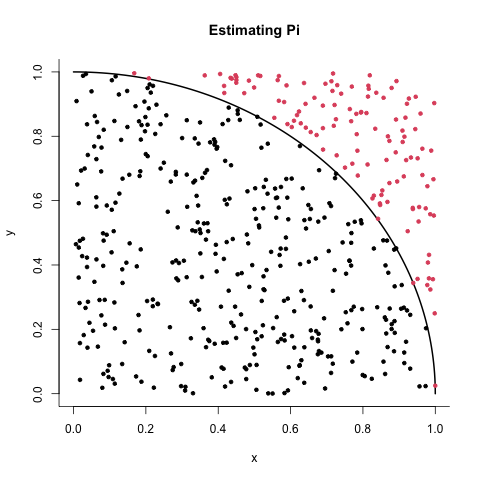
../../_images/85c2f2128db27c288effda72f2fe1a8c3588916c28ced5f52c7da7eb63e01c55.png

An implementation of this procedure in R is as follows:

%%R
pi_R <- function(n) {
  
  # we want n points, each point is in 2D space, so we need to sample m = 2*n
  # points using runif()
  m <-  2*n
  
  # get m samples - each sample is a row of the matrix 
  samples <- runif(m) |>
    matrix(ncol = 2)
  
  # how many lie inside the quarter circle?
  # get the distance between each row and the origin (0,0)
  n_inside_circle <- sum(sqrt(rowSums(samples^2)) < 1)
  
  # estimate pi by multiplying the proportion of points inside the quarter
  # circle by 4
  pi_estimate <- (n_inside_circle/n) * 4
}

Now, we can run the function for increasing $n$, which should converge to the true value of $\pi$.

%%R
# Estimates for different n
pi_estimate_1 <- pi_R(1)
pi_estimate_10 <- pi_R(10)
pi_estimate_100 <- pi_R(100)
pi_estimate_1000 <- pi_R(1000)
pi_estimate_10000 <- pi_R(10000)

pi_vec <- c(pi_estimate_1,
            pi_estimate_10,
            pi_estimate_100,
            pi_estimate_1000,
            pi_estimate_10000)

print(pi_vec)

[1] 4.0000 3.2000 3.1200 3.1640 3.1464

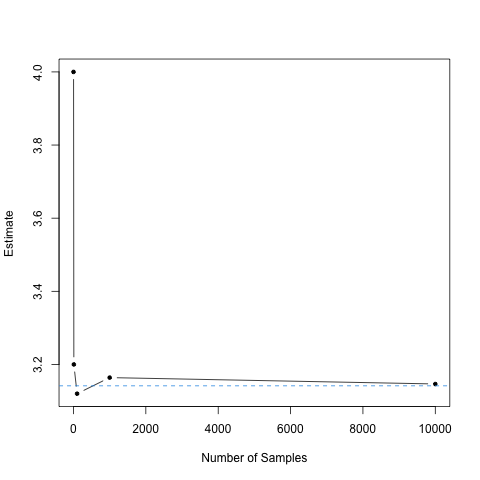
We can also plot the estimates, and compare them to the value of $\pi$ contained in R, which is accessible through pi and is denoted by the dashed horizontal line.

%%R
plot(c(1,10,100,1000, 10000), 
     pi_vec, 
     type ='b', 
     pch = 20,
     xlab = "Number of Samples",
     ylab = "Estimate")
abline(h = pi, col = 4, lty = 2)
../../_images/17ba3347311893431d09cdadca1c3a38321c0c5bce23918a24929dc9b7b6c3db.png

Suppose we want to do the same in C++. We can write the C++ code in a seperate file with a .cpp, then call it within R using the sourceCpp() function provided in the Rcpp package. For completeness, the C++ source code contained in the file pi.cpp is as follows:

Loading the function into R is as simple as calling sourceCpp():

%%R
sourceCpp("pi.cpp")

We can now run the function:

%%R
pi_cpp(10000)

[1] 3.1368

Finally, let’s compare it with the R implementation using microbencmark:

%%R
results <- microbenchmark(pi_R(1e6), pi_cpp(1e6))
summary(results)

           expr       min        lq      mean    median       uq      max neval
1   pi_R(1e+06) 13.200319 13.955457 14.982102 14.191412 14.81519 26.64340   100
2 pi_cpp(1e+06)  8.339154  8.391716  8.683018  8.419248  8.49766 16.95912   100

In addition: Warning message:
In microbenchmark(pi_R(1e+06), pi_cpp(1e+06)) :
  less accurate nanosecond times to avoid potential integer overflows

The C++ version is about twice as fast as the R version using 1e6 samples.

Contents